Cantilever Beams with Udl on Left Portion:

Consider a cantilever beam loaded with a Udl of w/unit length on portion AC as shown in Figure (a).

The Udl is added in both directions on the portion CB as illustrated in Figure (b).

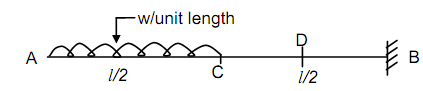
(a)

(b)

Figure

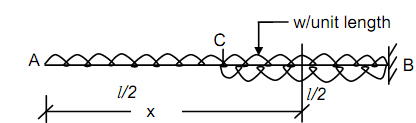
Consider a section X-X at a distance x from left end,

Moment, M =- w . x . (x/2) + w (x - (l/2)  ( x - (l/2))

 =- w x²/2 +(w/2)[x-(l/2)]²                    (Hogging BM)

The governing equation for deflection is :

EI d ² y/ dx²      = M = - w x²/2+(w/2)[x-(l/2)]²    

Integrating the Eq. (135), we can get

EI (dy/dx)         = - w x²/6+(w/6)[x-(l/2)] ³  +C₁  

EI y      = - w x²/24+(w/24)[x-(l/2)]²⁴  +C₁x+C₂  

The constants C₁ and C₂ can be found from boundary conditions. The boundary conditions are :

 At B,           x = l,            dy/ dx  = 0              ------------ (1)

 At B,              x = l,           y = 0                            --------- (2)

Applying the boundary condition (1) into the Eq. (136), we may get

0 = - wl ³/6 +   (w/6)(l-(l/2)³+C₁

∴          C₁ =   wl³/ 6[1-(1/8)]= 7 wl³/48

Applying the boundary condition (2) and value of C₁ into the Eq. (137), we may get

0 =- wl ⁴/24 +  (w/24)(l-(l/2))⁴  -7 wl 4 / 48   + C₂

∴          C₂  = wl ⁴ /24   [1 -( 1/16) - (7/2) ]  = wl ⁴/ (24 × 16) (16 - 1 - 56)

=- 39 wl ⁴ /(24 × 16)

C₂  = - 39 wl ⁴ /384

 The slope and deflection equations shall be :

EI (dy/dx)         = - w x³/6+(w/6)[x-(l/2)] ³  +7   w x³ /48       

EI y      = - w x⁴/24+(w/24)[x-(l/2)] ⁴  +7   w x³ /48  x-39wl⁴/384     

 Slope at A, (x = 0),

θ_A = + 7 wl ³ / 48 EI

Slope at C ( x = l/2) ,

EI θ_C = -(w/6)(1/2)3+  7 w l³/48 EI + = +6 w l ³/48 EI

Deflection at D (x = 3l /4) ,

EI θ_D = - (w/6) (   3l /4)3  +  (w/6) [ 3l/ 4  -(l/ 2)] + 7 wl³ /48

=- 27 wl³/24 × 16 + wl ³/24 × 16 +7 wl ³ /48

= wl ³/(24 × 16) [- 27 + 1 + 56] =30 wl3/384 = + 5 wl3/64

∴          θ _D       = +5 wl 3   /64 EI

Deflection at A, (x = 0)

y_C  =- 39 wl 4 /384 EI

Deflection at C, (x = l/2)

EI y_C  =- (w/24) (l/ 2) 4      +7 w l³/48  ×(l/2) -39 w l ⁴ /384

=( wl ⁴/384) [- 1 + 28 - 39] = - 12 wl ⁴ /384

∴          y          =- (12/384 ) (wl 4/  EI)

Deflection at D, (x = 3l/4)

EI yD  =- (w/24) (3l/4)⁴+  (w/24) [(3l/4)-(l/2)]⁴  + (7 w l³  /48)( 3l/4)- (39 wl ⁴/384)

= wl 4/24 × 256 [- 18 + 1 + 21 × 32 - 39 × 16]

= - 32 wl⁴ /(24 × 256) = -   (2/384 )wl 4

yD  = (wl ⁴ /192)     (w l ⁴/  EI)