Tangents at the Origin :

Let the equation of the parabolic curve passing through the origin point be

(a₁x + a₂y) + (b₁x² + b₂xy + b₃y²) + .... + (l₁xⁿ + ... + l_nyⁿ) = 0                  (1)

Let P (x, y) be any arbitrary point on the curve. The slope of the chord OP is y/x. Therefore the equation of the chord OP is

Y =(y/x)X .

As x->0, the chord OP happens to the tangent at O and so the equation of the tangent at O is

  

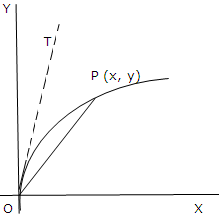
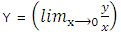
Y = mX, where m = lim_x->0 y/x.             (2)

Dividing (1) by x, we calculate


 
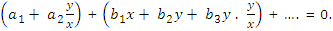
Taking the limit as x->0 and using (2), we take

a₁ + a₂m = 0

i.e. a₁ + a₂ Y/X = 0           (? Y = mX)

i.e. a₁X + a₂Y = 0.

Thus the equation of the tangent at the origin point can be shown as

a₁x + a₂y = 0.

That equation is similar as the lowest degree terms in (1) when equated to zero.

If a₁ = a₂ = 0, then (1) converts to

(b₁x + b₂xy + b₃y²) + (c₁x³ + c₂x²y + c₃xy² + c₄y³) + .... = 0           (3)

Dividing the x² and taking the limit as x->0, we obtain

b₁ + b₂m + b₃m² = 0

Or, b₁ + 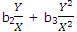 = 0 (? Y = mX)

Or, b₁X² + b₂XY + b₃Y² = 0.

We can write it as

b₁ x² + b₂xy + b₃y² = 0.                               (4)

which shows a pair of tangents at this origin.

The equation (4) is similar as the lowest degree terms in (3) when computed to zero.

Similarly, it may be shown that if a₁ = a₂ = 0 and b₁ = b₂ = b₃ = 0, then c₁x³ + c₂x²y + c₃xy² + c₄y³ = 0 is the equation of the curve tangent at the origin. Hence we have the given equation:

Rule: The tangents at the origin point are provided by equating to zero the lowest degree components in the equation of the provided curve.