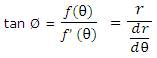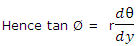Radius Vector, Tangent Angle:

Let P (r, θ) be any arbitrary point on the curve r = ƒ(θ). The angle in between the radius vector and the tangent TPT' at P is generally shown by Ø.        

 
                                           
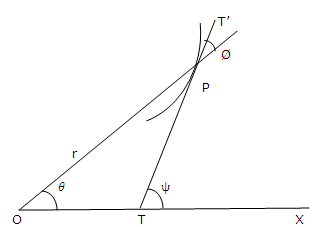
Let ∠XTP = ψ. Then tan ψ = dy/dx                               (1)

It is clear seen from the figure that ψ = θ + Ø                       (2)

If (x, y) are the Cartesian co-ordinates of P, then

x = r cosθ, 

y = r sinθ  

or, x = ƒ(θ) cosθ  ,

y = ƒ(θ) sinθ 

These can be regarded as parametric equations of the provided curve, θ being the parameter. We have

dx/dθ = ƒ' (θ) cosθ- ƒ(θ) sinθ 

dx/dθ = ƒ' (θ) cos θ+ ƒ(θ) sinθ

 
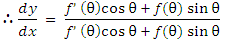
Dividing the denominator and the numerator by ƒ' (θ) cosθ and using (1), we get

 
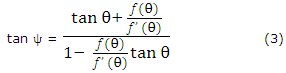
from (2), we get
 
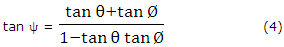
It follows from (3) and (4) that