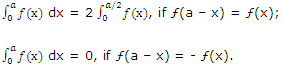Properties Definite Integrals:

We provide properties of a definite integral which enable us to calculate certain kinds of integrals.

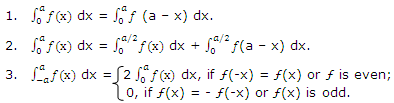
Proof: 1: Put a - x = y => dx = -dy.

We have y = a when x = 0 and y = 0 when x = a.

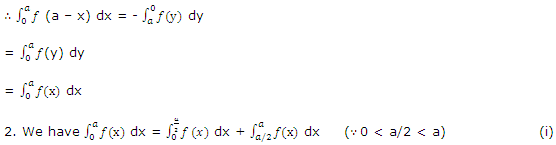
 Put x = a - y => ax = -ay.

2. We have y = 0 when x = a and y = a/2 when x = a/2.

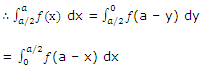
Thus by (i),

 
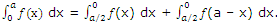
3. We get  

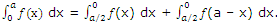
Put x = - y => dx = - dy.

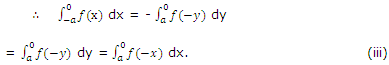
From (ii) and (iii), we get

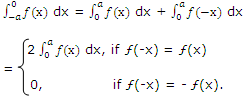
A function ƒ(x) is known as an even function if ƒ(-x) = ƒ(x). A function ƒ(x) is known as an odd function if ƒ(-x) = - ƒ(x). For example, x² and cos x are even functions; x², sin x are odd functions.

Corollary: It readily takes from property 2 that