Integral Fundamental Theorem:

If ƒ(x) is continuous in [a, b] and if F(x) is an integral of ƒ(x), then

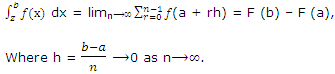
Proof: Let the interval [a, b] be divided into n similar parts, each of length h, by means of the points

a, a + h, a + 2h, ...., a + (n - 1) h, a + nh = b.

Since F(x) is an integral of ƒ(x),

∴ F'(x) = ƒ(x)     V x ->[a, b]

 
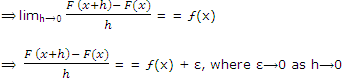
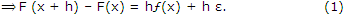
replacing x = a, a + h, a + 2h, ...., a + (n - 1) h respectively in (1), we get

F (a + h) - F (a) = hƒ(a) + h ε₁,

F (a + 2h) - F(a + h) = hƒ(a + h) + h ε₂,

F (a + 3h) - F(a + 2h) = hƒ(a + 2h) + h ε₃,

F (a + nh) - F [a + (n - 1) h] = hƒ [a + (n - 1) h] + h ε_n

Adding these relations, we obtain

F (b) - F (a) = h[ƒ(a) + ƒ(a + h) + .... + ƒ (a + (n - 1) h)] + h (ε₁ + ε₂ + ... + ε_n) (? a + nh = b)                   (1)

Let ε_k (1 ≤ k ≤ n) be such that |ε_i| ≤ |ε_k| ;  i = 1, 2, .... , n.

h (ε₁ + ε₂ + ... + ε_n) ≤ hn |ε_k| = (b - a) |ε_k|   (? a + nh = b) 

since ε_k ->0 as h->0, it follows that

h |ε₁ + ε₂ + ... + ε_n| ->0as .

Thus on taking the limit as n->∞ in (1), we get

F (b) - F (a) =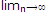 [ƒ(a) + ƒ(a + h) + .... + ƒ{a + (n + 1) h}].

 
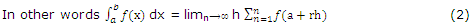
Remark: the relation (2) can be shown as

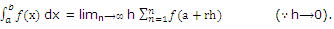
= lim h [ƒ(a + h) + ƒ(a + 2h) + .... + ƒ(a + nh)]

where h->0 ,n->0 and nh = b - a.