Homogeneous Reducible Equation:

Type 1: Suppose a differential equation of the form:

 
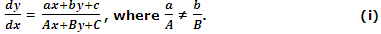
 That is clearly non-homogeneous. In order to create it homogeneous, we proceed as follows:

We replace x = X + h and y = Y + k in (i), where h, k are constants to be calculated suitably.

 
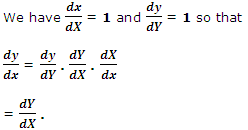
 Now (i) becomes

Select h and k so that

ah + bk + c = 0,

Ah + Bk + C = 0.

These equations provide

 
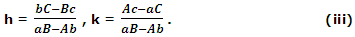
 Now equation (ii) becomes

 
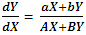
 which being a homogeneous equation will be solved by means of the replacement Y = VX.

Type II: Suppose a differential equation of the form

 
 Since aB - Ab = 0, the above function fails in view of (iii).

We have

 

Let us replace Ax + By = z such that

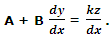
Now (iv) becomes

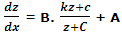
which is an equation with different variables.