Exponential Function:

The function y = ax (a > 0 and a ≠ 1), where x is a real number, is known as an exponential function with base a.

Suppose a be any positive real number and n be any positive integer.

We described an as follows:

aⁿ = a × a × .... × a (n times)

It follows from the meaning that,
   
(i) a^m aⁿ  = a^m+n,
       

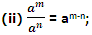
(iii) (a^m)ⁿ = a^mn

Where n and m are positive integers. Notice that m > n in (ii).

The above definition is simply extended to all integers by defining,

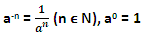
For a positive rational number m/n, we describe a^m/n as the nth root of the mth power of a i.e. 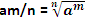 and

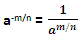
If x is any real number, we describe

 
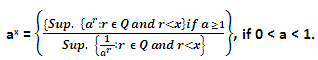
 It can observed that since the set {a^r : r ? Q and r < x} is bounded and non-empty above for a > 1, therefore, by the order completeness charters tics of R, the supremum of the set exists.