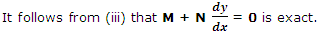Exact Differential Equation:

A first order differential equation

 
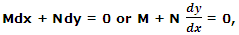
 where M and N are functions of x and y, is called exact if there exists some function ƒ (x, y) such that

 
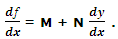
 In that case ƒ (x, y) = c is the basic solution of the provided differential equation.

 
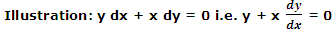
 is an exact differential equation, since

 
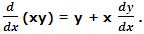
Theorem: The enough and necessary condition for the equation Mdx + Ndy = 0 to be exact is

 
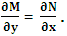
Proof: (Necessary Condition)

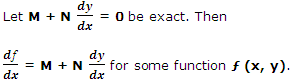
(Sufficient Condition)

 

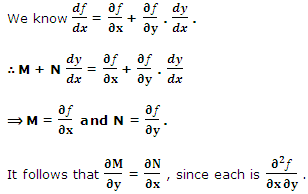
Let U = ∫M dx, where y is saved as a constant in M.                              (i)

 
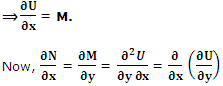
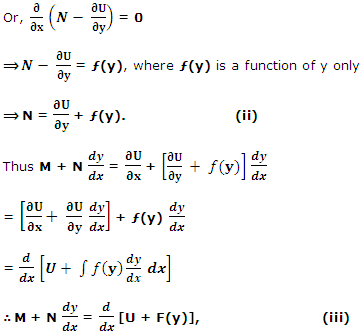
 Where F(y) = ∫ƒ(y) dy.                                (iv)