Equations Solvable for y:

Suppose the equation F (x, y, p, ...., p_n) = 0 on solving for y is expressible as

y = ƒ(x, p).                                  (i)

Differentiating (i) w.r.t. x, we obtain an equation of the form

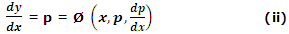
which is a differential relation in two variables p and x.

Suppose the solution of (ii) is ψ (x, p, c) = 0.                  (iii)

Now to get the solution of the given differential equation, we may either eliminate p between (i) and (iii) or we may solve (i) and (iii) for x and y in term of p. In the last case,

x = ƒ₁ (p, c), y = ƒ₂ (p, c); (p being a parameter) is the required solution.