Elementary Functions Continuity:

Theorem: All Elementary or basic functions are continuous in their related domains.

Proof: (i) power function y = xⁿ (n is an integer). If n is a positive value, then ƒ(x) = xⁿ being a polynomial function is continuous in R. computing by theorem, it follows that,

x^-n = 1/xⁿ (n > 0)

is continuous in R ~ {0}.

(ii) Trigonometric and inverse trigonometric functions: we known that sin x and cos x are continuous in R. Thus by Theorem,

tan x = sin x/ cos x is continuous in

R ~ {(2k + 1) π/2: k = 0, ±1, ±2, ....}

Same as cot x, sec x and cosec x are continuous in their related domains. It now follows by Theorem that sin ^-1 x, cos^-1 x, tan^-1 x, cot-1 x, cosec^-1 x and sec^-1 x are also continuous in their related domains.

(iii) Exponential and logarithmic functions: Suppose x₀ be any number. We have

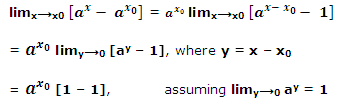
= 0

 
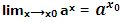
 Thus, y = a^x is continuous in R. calculating by Theorem, it follows that its inverse function y = log_a, x is continuous in ]0, ∞[.