Differential First Order Degree:

The general form of a differential equation of first degree and first order is

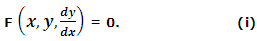
By a solution of the differential equation (i), we denote any function y = ƒ(x) such that F (x, ƒ(x), ƒ'(x)) = 0 holds identically.

Suppose the differential equation:

dy/dx = cos x.                                (ii)

Then y = sin x is a solution of (ii). We see that y = sin x + 1, y = sin x - 3 are also solutions of (ii). The solution y = sin x + c, where c is an arbitrary constant, is called as the general solution of (ii), since each and every solution of (ii) may be calculated from y = sin x + c for a suitable selection of c.

The relation y = Ø (x, c), where c is an arbitrary constant, is known as the general solution of

 
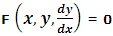
 If every solution of the above equation is provided by y = Ø (x, c) for a suitable selection of c.

Usually, the solution of a differential equation which has a number of arbitrary constants same to the order of the differential equation is known as the general solution. Thus the universal solution of a differential equation of the nth order has n arbitrary constants.

A solution calculated from the basic solution by giving several values to the constants is known as a particular solution.