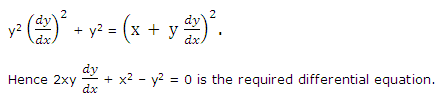Differential Equation Formation

Let ƒ (x, y, c₁, c₂, ...., c_n) = 0     ........(1)

be the computation of a differential equation, where c₁, c₂, ...., c_n are n arbitrary constants. If we remove these n constants, we calculate the differential equation of the n^th order fulfilled by (1). The equation (1) taken together with n relations calculated by differentiating (1) n times helps us to remove the n constants.

Example: By the removal of the constant a, get the differential equation of which (x - a)² + y² = a² is the solution.

Solution: differentiating (x - a)² + y² = a² w.r.t. x,

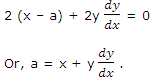
Replacing in (1), we obtain