Derivative Differentiation:

The derivative of a function is important tool in mathematics. The motion of derivative was produced to solve problems of Physics concerning motion of an object. The velocity of a body is a calculation of the rate of change of distance with respect to time. Acceleration is a calculation of the rate of change of velocity with respect to time. That rate of modification is precisely provided by the motion of derivative. The derivative is also used to find tangent lines to curves.

The concept of derivative has been applied to other fields as well. A biologist uses it to calculate the rate of growth of bacteria in a nature. An economist uses it to solve problems dealing with profits and losses of a company. An electrical engineer needs it to define the change in current in an electric circuit.

Derivative of a function at a point

The derivative of a function ƒ at a point x = c, shown by ƒ'(c), described as

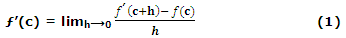
given the limits exists

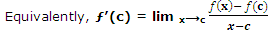
[Take c + h = x in (1)].

If ƒ has finite derivative at any point, ƒ is called differentiable or derivable at that point. The derivative of a function is also known as its differential coefficient. The process of finding out the derivative of a function is known as differentiation.