Derivability and Continuity:
Theorem: If a function ƒ is derivable at an arbitrary point, it is continuous at that point.
Proof: Let ƒ be derivable at arbitrary point x = c. Then
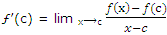
exists and is finite. Now,
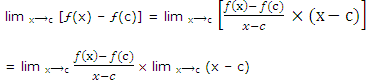
∴ ƒ'(c)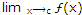 
= ƒ(c). Thus ƒ is continuous at x = c.
Remark: the converse of the given theorem is not true. A function can be continuous at point without being derivable at that point.