Definite Integral:

If F(x) is an integral of ƒ(x), then the symbol

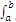 [ƒ(x)] dx is denoted as F (b) - F (a).

The expression F (b) - F (a) is also shown by |F (x)|^b_a .

Therefore

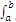  [ƒ(x)] dx = |F (x)|ba  = F (b) - F (a).

We see that

|F (x) + c|ba  = [F (b) + c] - [F (a) + c]

= F (b) - F (a)
 
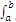  [ƒ(x)] dx.

Hence 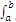 [ƒ(x)] dx is independent of the selection of the constant of integration 'c' and so we known 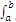[ƒ(x)] dx as definite integral.

We call it as integral of ƒ(x) from a to b. The number a is known as the lower limit and the number b is known as the upper limit of integration.

Remark: If we give a substitution t = Ø(x) in a definite integral 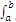 [ƒ(x)] dx, the changed definite integral can be from t = Ø(a) to Ø(b).