Curves Family Envelope:

A curve which touches each and every member of a family of curves and which is touched at every point by some member of the family is known as the envelope of the family of curves.

Example: Suppose the family of straight lines

y = mx + a/m ,

where m is the parameter and a is some constant.

We know that each and every member of the family touches the parabolic y² = 4ax. Also the parabola y² = 4ax has at each point the tangent which is of the form y = mx + a/m . Thus y² = 4ax is the envelope of the provided family of lines.

The cover of a family of curves

Ø (x, y, α) = 0,

If it exists, is get by solving simultaneously the equations

Ø (x, y,α ) = 0   and  Øα (x, y, α) = 0

Proof: the provided family of curves is

Ø (x, y, α) = 0.                                (1)

Take the parametric equations of the envelope be

X = ƒ(α),    y = g(α).

Then Ø ƒ(α), g(α), (α) = 0 identically.       (2)

Differentiating (2) w.r.t. α(Supposing that Ø, ƒ and g have continuous derivatives.)

Øx ƒ' (α) + Øy g' (α) + Øα = 0                  (3)

By (1), Øx + Øy dy/dx = 0

Thus the tangent of any member of the family Ø (x, y, α) = 0 at (x, y) is shown by

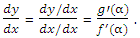
Or Øx ƒ' (α) + Øy g' (α) = 0.                       (4)

On comparing (3) and (4), it follows that

Ø α= 0

That proves the theorem.

Remark: The cover of a family of curves Ø (x, y, α) = 0 can also be calculated by eliminating α between Ø (x, y, α) = 0 and Øα (x, y, α) = 0.