Chain Rule Function Derivative:
Theorem: Suppose g(x) be derivable at x and that y = ƒ(u) be derivable at the corresponding value of (u). Then the compound function y = ƒ (g (x)) is derivable at x and
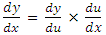
Proof: Let Δy and Δu be the increments of y and u respectively corresponding to the increments Δx of x. The relation
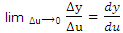
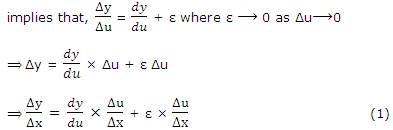
Since u is derivable at x, it is continuous at x and so
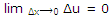
taking the limit as in (1), we get
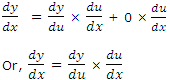
which proves the theorem.