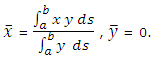Centre of Gravity-Volume:

Let an arc AB of the curve y = ƒ(x), enclosed by two ordinates x = a, x = b, and x-axis, revolve about x-axis. The volume prepared by the revolution about x-axis of the area PMNQ is a disc of radius y and thickness Δx. The volume of that disc is π y² Δx and its C.G. is at (x, 0), where Δx is indefinitely very small. Therefore the co-ordinates of the C.G. of the volume of revolution get on revolving the arc AB about x-axis are

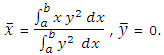
Now the surface produced by the revolution of the arc PQ = Δs about x-axis is a ring of radius y with centre at (x, 0). The surface area of that ring is 2πy Δs and its C.G. is at (x, 0). Therefore the co-ordinates of the C.G. of the surface of revolution get by revolving the arc AB about x-axis are