Centre of Curvature:
Definition 1: The centre of curvature of any curve at any point P is the point C which takes on the normal at P drawn in the path of the concavity of the curve such that CP = ρ, where ρ is the radius of curvature of the curve at P.
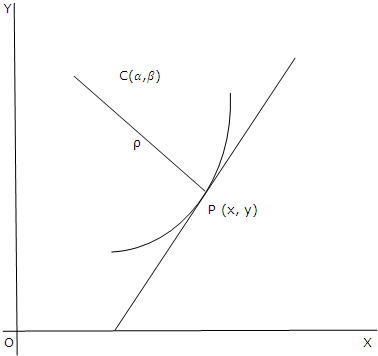
Definition 2: the circle of curvature of any curve at any point P is the circle (passing through P) whose radius ρ and centre of curvature (at P), ρ being the radius of curvature at P.
Definition 3: (Evolute and Involute)
The locus of centers of curvature of a curve is known as the evolute and the provided curve is known as the involute.
The co-ordinates of the centre of curvature
Consider that C is the centre of curvature of the curve y = ƒ(x) at any arbitrary point P(x, y). The equation of the normal to the curve at P is
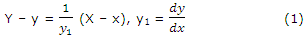
By definition C lies on (1), therefore

Since CP = ρ, (α - x)2 + (β - y)2 = ρ2 (3)
Replacing (2) in (3), we obtain
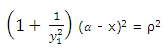

from (4) and (2), we get
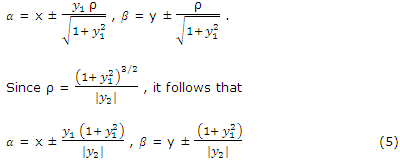
Case I: Let y2 > 0 such that the curve is concave upward at P. Then α< x and β> y. Therefore, by (5) the coordinates of the centre of curvature are
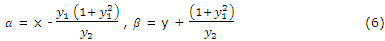
Case II: let y2 < 0 so that the curve is concave downward at P. It may be shown that the coordinates of the centre of curvature are the similar as given in (6).