Cartesian Curve Tracing:

 The subsequent steps are very needful in tracing a Cartesian curve ƒ(x, y) = 0.

1. Symmetry
   
(i) The curve is symmetrical related to x-axis if all powers of y in the equation of the provided curve are even [?ƒ(x, y) = ƒ(x, -y)].
   
(ii) The curve is symmetrical related to y-axis if all powers of x in the equation of the provided curve are even [?ƒ(x, y) = ƒ(-x, y)].
   
(iii) The curve is symmetrical related to the line y = x if the equation of the provided curve remains unaffected on interchanging x and y.
   
2. Origin

Search out if the origin lies on the curve. If it does, find out the tangents or tangent at the origin. In that case the origin is a multiple point, search out its nature.
   
3. Intersection with the co-ordinate axes

Search out the points of intersection of the curve with co-ordinate axes and the tangents at such points.
   
4. Asymptotes

Search out the asymptotes of the curve.
   
5. Region

Search out the sections of the plane in which no part of the curve lies. To calculate such regions we solve the provided equation for y in terms of x or vice-versa. Consider that y becomes imaginary for x > a, the curve does not laze in the region x > a.
   
6. Solving the equation

If possible, Compute the equation of the provided curve for y in terms of x and observe how y varies from -∞ to +∞.
   
7. Critical points

Search out the values of x at which dy/dt = 0.

At that points y usually changes its character from an decreasing function of x or increasing function of x to or vice-versa.
   
8. Points of inflexion
Search out the points of inflexion (provided by 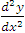) and the sections of concavity and convexity of the curve.