Asymptotes:

If a curve is arbitrarily nearer to an infinite segment of a line L, then L is known as an asymptote of the curve. Equivalently, we provide the following:

 
Definition: The line y = mx + c (m ≠ 0) is called as an asymptote of a curve y = ƒ(x) if the perpendicular distance of any arbitrary point P(x, y) on the curve from the line tends to zero as x -> ∞ + or - ∞.

We shall now calculate the conditions in order that the line

y = mx + c

is an asymptote of the curve y = ƒ(x). If p shows the perpendicular distance of any point P(x, y) on the curve from the line, then

 

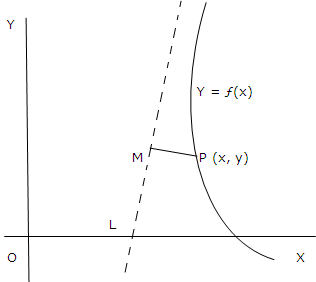
By definition p →0 as x → ± ∞

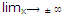=>  (y - mx - c) = 0                                                               (i)

 

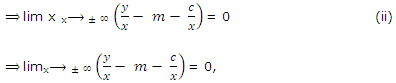
Since otherwise the limit in (ii) could be 
 

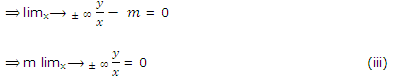
This calculates the value of m. Now, by (i), we have

c = m 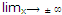(y - mx)                                                                       (iv)

This calculates the value of c.

Rule: The line y = mx + c (m ≠ 0) is an asymptote of the curve y = ƒ(x), where m and c are calculated by

m 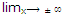 y/x ,c =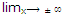(y - mx).