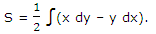Area Bounded by Closed Curve:
The area surrounded by a closed curve provided by x = ƒ(t), y = g(t); t1 ≤ t ≤ t2 is
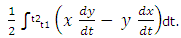
Proof: Let AP1 BP2 be the provided closed curve which does not intersect itself. Let the curve be intersecting by a line parallel to the y-axis in two and only two arbitrary points P1, P2. Let MP2 > MP1. Let BD and AC be two tangents at B and A respectively which are parallel to the y-axis. Take OC = a, OD = b.
If S is the area of the bounded region AP1 BP2, then S = S1 - S2, where
S1 = Area of the bounded region CDBP2A
And S2 = Area of the bounded region CDBP1A.
Consider that as t increases from t1 to t2, the points (x, y) going from an arbitrary point E on the curve returns to the point E when taken in counter-clockwise direction. Since the curve is end, the point on it which related to t = t1 is the similar as the point which relates to t = t2. Let the values of t equivalent to A and B be ta and tb, respectively.
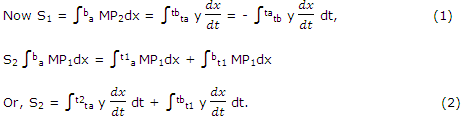
It follows, from (1) and (2),
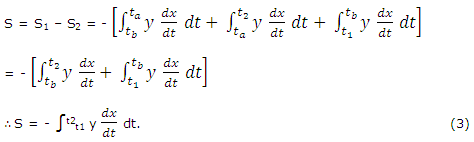
Same as, by drawing the tangents parallel to the x-axis and operating the formula ∫x dy for the area bounded by a region, the y-axis and to abscissa, we may show that

Adding (3) and (4) and dividing by 2, we get
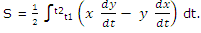
This is often shown as