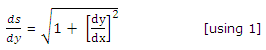Arc Length Derivative:

Let P (x, y) be any arbitrary point on a given curve y = ƒ(x). Let s indicates the arc length calculated from a fixed point A on the given curve to the point P i.e. arc AP = s. Consider that s increases as x increases. Clearly s is a function of x. We get a neighboring point Q (x + Δx, y + Δy).
 

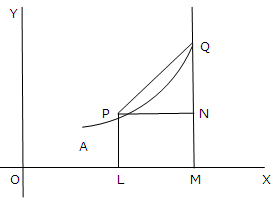
Let AQ = s + Δs

∴ Arc PQ = Δs

We can assume that
 
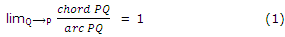
from the right-angled ΔPQN, we have
 
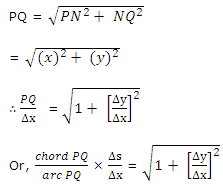
Taking the limit as Q → P (or Δx → 0), we obtain