Algebraic Curves Asymptotes:

The equation of an algebraic bounded curve of degree n is of the form

(a₀xⁿ + a₁x^n-1 y + ... + a_n yⁿ) + (b₀x^n-1 + b₁x^n-2 y + .... + b_n-1 y^n-1) + ... + (ax + by) + c = 0.

This may be written as
 

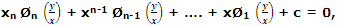
Where 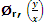 is a polynomial in of degree r.

Asymptotes parallel to the ordinate axes

Let the equation of the curve be shown as

yⁿ Ø(x) + y^n-1 Ø₁(x) + y^n-2 Ø₂(x) + ... + yØ_n-1 (x) + Ø_n (x) = 0,                               (1)

where Ø(x), Ø₁(x), ......, Ø_n(x) are polynomials in x.

Dividing (1) by yⁿ, we get

 

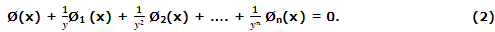
Let x = a be a vertical asymptote of (1) such that

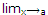 y = ±∞, now it takes from (2), Ø(a) = 0.

Thus, 'a' is not root of Ø(x) = 0 which shows that (x - a) is a factor of Ø(x). Hence we have the subsequent:

Rule 1: The asymptotes parallel to the y-axis of an algebraic curve or vertical asymptotes are get by equating to zero the real linear factors on the coefficient of the highest power of y in the equation of the provided curve.

Same as, we have

Rule 2: The asymptotes parallel to the x-axis or the horizontal asymptotes of an algebraic curve are get by equating to zero the real linear factors in the coefficient of the highest power of x in the equation of the provided curve.