Total horizontal pressure:

Total horizontal pressure P = 30 × 6/2 = 90 kN acts at a height of 6/3 = 2 m from the bottom edge C.

If the width of a base of the wall for no tension is 'b' then weight of 1 m width of wall 23 × 1 × (1 + b/2 × 6 ) kN = 69 (1 + b) kN.

It acts by x¯  where x¯  is the distance of CG of this trapezium ABCD from line BC.

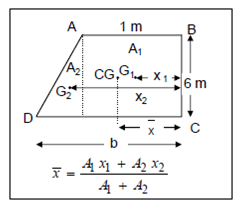
x¯ = 1 × 6 × 0.5 + (b - 1) × (6/2) × (b-1/3) +1/1 × 6 + (b - 1) × 6/2

b² + b + 1/3 (b + 1)

A weight line GE meets the wall base CD; at E such that

EC = b²+b+1/3(b+1), DE =b-EC = 2b²+2b-1/3(b+1)

Hence, eccentricity (e) of the weight,

OE =DE-DO = 2b²+2b-1/3(b+1) - b/2 = b²+b-2/6(b+1)

The net bending moment at base, M = P ⋅ h/3 - W ⋅ OE

= 90 × 2 - 69 (1 + b) b²+ b - 2/6 (1 + b) = 180 - 11.5 (b² + b - 2) kNm

∴ Minimum bending stress at C =   W/ b × 1 - (M. b/2)/ 1 × b³/12  = W/b - 6 M/ b²

69 (1 + b)/b - (1080/b² -69(b²+b-2/b²))

Here for no tension at base DC the above stress at C must be zero

∴          69 (1 + b)/b= 1080/b² - 69 (b² + b - 2)/b²

giving,            b (1 + b) = 15.652 - (b² + b - 2)

or,       b² + b - 8.826 = 0

Giving b = - 1 ± 6.025/2 = 2.513 m (taking the positive value)

Hence take the base width as 2.6 m.

Maximum pressure at base at point D is

69 (1 + 2.513)/ 2.513 + 6 × [180 - (2.513³ + 2.513 - 2) × 11.5/ 2.513²

 96.46 + 96.46 = 192.92 kN/m²