Find out the value of the maximum pressure:

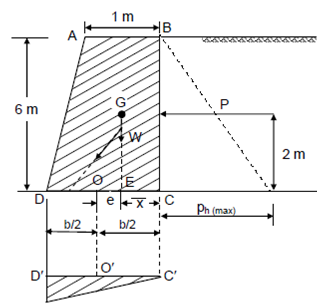
A masonry retaining wall of trapezoidal section retains level earth 6 metres high. The retaining wall is 1 m wide at the top, determine the bottom width so that no tension is induced in the base. The unit weight of masonry is 23 kN/m³ and of soil 15 kN/m³. The angle of repose of the soil is 30^o and the back face of the wall is vertical.

Figure

Find out the value of the maximum pressure at the base.

Solution

A horizontal pressure p_h at any depth h is given by

p_h   = w. h ⋅ 1 - sin φ/1 + sin φ 1= 15 × h  1-sin 30^o/1 + sin 30^o

p_h = 15 ×1/3 h =  5 h (kN/m² )

p_h(max) = 5 × 6 = 30 kN/m² (at h = 6 m) at base

Considering 1 m width of the wall.

Total horizontal pressure P = 30 × 6/2 = 90 kN acts at a height of 6/3 = 2 m from the bottom edge C.

If the width of a base of the wall for no tension is 'b' then weight of 1 m width of wall 23 × 1 × (1 + b/2 × 6 ) kN = 69 (1 + b) kN.

It acts by x¯  where x¯  is the distance of CG of this trapezium ABCD from line BC.