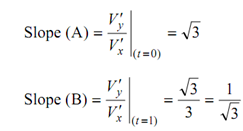Find out and plot the equation of Hermite form of the cubic spline:

Find out and plot the equation of Hermite form of the cubic spline from given position vectors and slopes at the data points with vector magnitude equal to 1.

Point 1 : A = [1, 2]^T, slope (A) = 60^o

Point 1 : B = [3, 1]^T, slope (B) = 30^o

Solution

In this instance, for simplicity, just one segment of Hermite cubic spline is considered.

V_x  = V_x (t ) = V_x (0) (1 - 3t ²  + 2t³ ) + Vx (1) (3t ²  - 2t³ )

+ Vx′ (0) (t - 2t ² + t³) + Vx′ (1) (- t ² + t³)

From the given data, we obtain

V_x (0) = 1,  V_x (1) = 3

As the magnitude of the tangent vector is 1,

V'_x (0) = 1 . cos 60,  V'_x (1) = 1 . cos 30

Upon substitution of these values in Equation V (t), we get

V_x  = 1 (1 - 3t ²  + 2t³ ) + 3 (3t ²  - 2t ³ ) + cos 60 (t - 2t ²  + t³ ) + cos 30 (- t ²  + t³ )

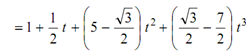
Likewise, from Equation V (t),

V_y  = V_y (t ) = V_y (0) (1 - 3t ²  + 2t³ ) + V_y (1) (3t ²  - 2t³ )

+ V_y′ (0) (t - 2t ²  + t ³ ) + Vy′ (1) (- t ²  + t ³ )

 Again, from the given data,

V_y (0) = 2,        V_y (1) = 1

V'_y (0) = 1 . sin 60,       V'_y (1) = 1 . sin 30

Upon substitution of these values in Equation V (t), we achieved

V_y  = 2 (1 - 3t ²  + 2t³ ) + 1 (3t ²  - 2t³ ) + cos 60 (t - 2t ²  + t³ ) + sin 30 (- t ²  + t ³ )

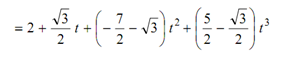
To examine it, we substitute t = 0, 1 into the previous equations; then

V (t = 0) = [1, 2],          V (t = 1) = [3, 1],