Trigger strategy:

Produce half of the monopol  output  (q_m/2)  in  the first period. Continue t  iY to produce  the same in  the t period  if both the  firms produced (q_m/2) in the t-1^th period; otherwise produce the Cournot output q_c.  

The profit to one firm when both the firms produce  (q_m/2)  is denoted by Π_m/2 Whereas the profit  accruing to each  firm when both  produce q_c  is denoted  by Π_c

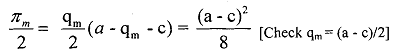
Finally, if firm  1 is going to produce  (qm/2)  this period, then the quantity that maximises j's  profit  in  this period,  is  obtained solving  the  following simple maximisation problem:

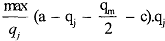
The  solution of  the problem  can  be  obtained from the first order condition of profit maximisation, that is,

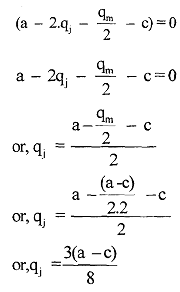
with  associated profit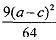 . We will denote this profit by Π_d (d  stands 64 for deviation). Therefore,  it  is  a Nash equilibrium for  both the  firms  to play  the  trigger strategy, given earlier provided that, present value of payoff from the trigger strategy ≥ present value of the payoffs deviated  in the first period.

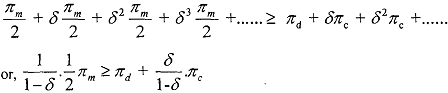
Substituting  the  values  of  Π_d and Π_d,  into  the above equation,  we  get  if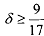,  then the  inequality will hold and the trigger strategy will be  sub-game 17 perfect.

Thus,  we  see that collusion  in  infinitely  repeated  games can fetch extra payoffs to the firms.