Friedmans theorem:

Friedman's theorem (1971)  is another milestone  in  determining  the existence of sub-game perfect Nash  equilibrium of an  infinitely repeated game G (a,  3). But before stating the theorem, we need to know a couple of definitions.

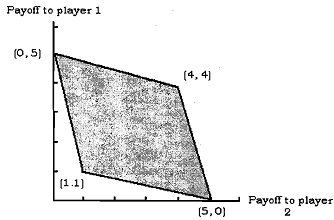
Feasible Payoff: We call the payoffs (x₁,  x₂,.., x_n)  feasible in  the stage game G  if  they  are  a  convex combination  (i.e.,  a  weighted average, where  the weights are non-negative and they sum up to one) of the pure-strategy payoffs of  G.  In the  following  diagram  we  present  the  feasible payoffs  of  the Prisoners'  dilemma game, by  the shaded region. The pure  strategy payoffs are feasible and they are (1, 1  ), (0, 5), (5, O),  (4,4). One can check that any payoff allocation  inside the shaded region can be  achieved  as a weighted  average of the pure strategy payoffs.  

Average payoff: Till now we defined players' payoff in an infinitely repeated game  to be  the  present  value of  the infinite sequence of  stage game payoff. But  it  is more convenient to express the present value  in  terms of the average payoff  from  the same infinite sequence of  stage game payoffs. The average payoff  of  an  infinitely  repeated game is  the  payoff  that would  have  to  be received  in  every  stage so as to  yield  the same present  value. Let  d be  the discount factor. Suppose  the  infinite sequence of payoffs 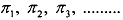 has  the present  value V.  If  the  payoff  rwere ,received in  every  stage,  the present value would  be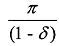. For  r  to  be  the average payoff  from  the infinite sequence, 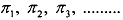with discount factor d,  the two present values must be equal, which gives n  = V.(1  - d  ). That is, the average payoff is  (1  - d )times the present value. Given  the  discount factor d,  the average  payoff of  the infinite sequence of

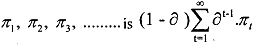
Friedman's Theorem: Let G be a finite static game of complete information. Let  (e₁,  e₂,  e₃,  .....e_n)  denote the payoff from a Nash equilibrium of G, and let (x₁, x₂,  x₃,  .....  x_n  ) denote any other payoffs from G. If xi  > ei  for every player  I  and  if  δ is  sufficiently close to one,  then  there  exists a  sub-game perfect  Nash  equilibrium  of  the infinitely  repeated game 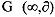 that achieves (x₁, x₂,  x₃,  .....  x_n) as the average payoff.

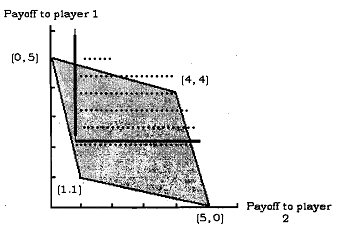
Friedman's  theorem  ensures that  any  point  in  the  dotted  area  in  the  above diagram can  be  achieved  as  the average payoff  in  a  sub-game  perfect Nash equilibrium  in  a  repeated  game, provided that  the  discount factor  is sufficiently close to one.