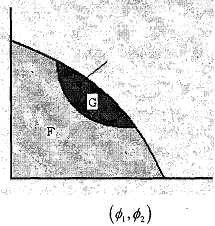
Axiom  of Independence  of Irrelevant Alternatives: 

For  any closed  set G, where G ⊆ F; and  Φ(F, v) ∈ G, Φ(G, v) = Φ(F,v).
We  illustrate  the above statement with a diagram.  

Axiom  of Symmetry:  If  v₁ = v₂  and  (x₂,x₁ | (X₁,X₂)∈F] = F  (that  is  F  is symmetric),  then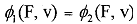 

The above statement implies equal players must be treated equally.

Using the above axioms, Nash derived a theorem:

There  is  a  unique  solution  function Φ(F, V)  that  satisfies all the  above- mentioned axioms, for every two person bargaining problem (F, v).