Axiom of Efliciency:

Suppose we have two vectors x and y: x =  (x₁. x₂)  and y =  (y₁.y₂)

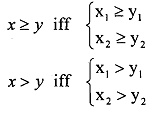
Φ (F, v)  is an allocation in  F and for any x in F
If x ≥ Φ(F, v),
then x = Φ(F, v).
This means the solution in a bargaining problem is always Pareto optimal.

Axiom of Individual Rationality:

Φ(F, v) ≥ v. This axiom means individuals are  rational.  They  do  not  accept  a  division  in  which they  get less  than  the disagreement payoff.

Axiom of Scale Covariance:

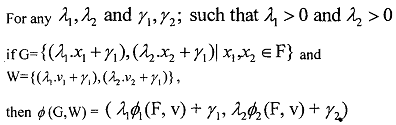
The above statement implies change of  origin and scale should not matter to the solution.