Bending Stress Due to Biaxial Bending:

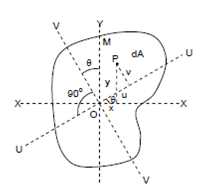
In Figure 8, the bending moment acts in the plane OM, where O is the centroid of the section and UU and VV are the principal axes of the section.

The plane OM in which the bending moment M lies makes an angle θ with the axis OV. Hence the resolved parts of M along OV and OU are M_u = M cos θ and M_v = M sin θ.

[Note:  Here mark that the moment in plane OV is called M_u since it bends the section about the perpendicular axis U-U, similarly M_v bends it about VV.]

Figure

If P is any point within the section, whose co-ordinates with reference to UU and VV are u, v after than the stress at P due to the component M cos θ is given by

f_u  =     M_u/I_uu × v =  M cos θ/I_uu × v

Same stress because of component M sin θ will be

fv   = (M sin θ / I_vv)u

And the total stress at P will be

f  = (M sin θ / I_vv)v + (M sin θ/ I_vv)u