Determine the points on the curve:

Make out the equation of a Bezier curve; determine the points on the curve for t = 0, 1/4, 1/2, 3/4, and 1 and plot the curve for the following data. The coordinates of the four control points specified by

V₀ = [0, 0, 0]

V₁ = [0, 2, 0]

V₂ = [4, 2, 0]

 V₃ = [4, 0, 0]

Solution

The number of control points is 4 (that is, 4 = n + 1), we set n = 3. Then we have the Bezier curve function as follows:

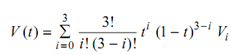
V (t ) = V₀ (1 - t)³  + 3V₁ t (1 - t )²  + 3V₂ t ²  (1 - t ) + V₃ t ³           0 ≤ t ≤ 1

Substituting the values t = 0, 1/4, 1/2, 3/4, 1 into this equation, we have

V (0) = V0 = [0, 0, 0]_T

V (1/4)     =    (27/64) V₀  +    (27/64) V ₁ +    (9/64) V ₂  +(1/64) V³  =,[(5/8),(9/8) , 0]^T

V (1/2)     =    (1/8) V₀  +        (3/8) V ₁ +        (3/8) V ₂  +(1/8) V³  =,[(2),(3/2) , 0]^T

V (3/4)     =    (1/64) V₀  +      (9/64) V ₁ +      (27/64) V ₂  =,[(22/8),(9/8) , 0]^T

V (1) = [4, 0, 0]^T