Linear Regression:

The process for obtaining the best fit is frequently called the "regression". Linear regression refers for straight line fitting of data.

Linear approximations are frequently satisfactory in an extensive variety of engineering applications.

If we choose a straight line for curve fitting as below:

f (x) = a + bx, where a and b are coefficients to be find out. Then for "best fit", the sum S which is to be minimized shall be

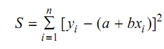
The minimum occurs when

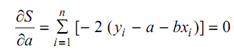
and

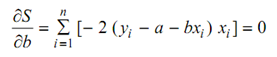
These can be simplified & expressed as

∑ y_i - ∑ a - ∑ b x_i = 0 and ∑ y_i x_i - ∑ a x_i - ∑ b    = 0

i.e.,         na + b ∑ x_i = ∑ y_i         and        a ∑ x_i  + b ∑   = ∑ x_i y

These two simultaneous equations might be solved to attained the coefficients a and

b. The resulting equation f (x) = a + bx then provides the best fit straight line to the given data. The spread of data before regression applied can be n,

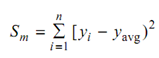
where y_avg can be average or mean of the given data. The extent of improvement because of curve fitting is given by the expression

                                    r ²  = (S_m  - S ) / S_m

where r is the correlation coefficient.

It can be noted down that r has a maximum value of 1.0. Its value will be superior for good correlation!