Application of Bernoulli's Equation to a Venturi

Most of the plant components, like a venturi, might be analyzed by using Bernoulli's equation and the continuity equation. The venturi is a flow measuring device which consists of a steady contraction followed by a steady expansion. An illustration of a venturi is shown in figure below. By measuring the differential pressure among the inlet of the venturi (i.e., point 1) and the throat of the venturi (i.e., point 2), the flow velocity and mass flow rate can be established depend on Bernoulli's equation.

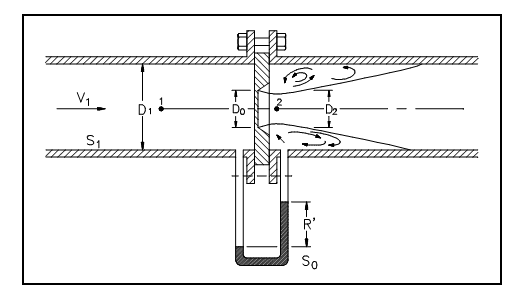
Figure: Venturi Meter

Bernoulli's equation defines that the total head of the flow should be constant. As the elevation does not change appreciably, when at all, among points 1 & 2, the elevation head at the two points will be necessarily similar and will cancel out of the equation. Therefore Bernoulli's equation simplifies to the below equation for a venturi.

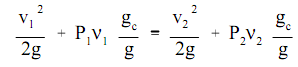
Exerting the continuity equation to points 1 and 2 permit us to express the flow velocity at point 1 as a function of the flow velocity at point 2 and the ratio of the two flow regions.

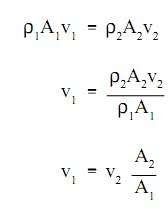
By using algebra to rearrange the above equation and replacing the above outcome for v₁ permits us to solve for v₂.

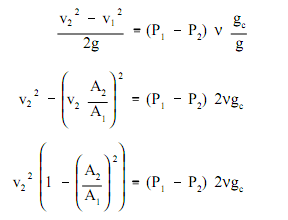
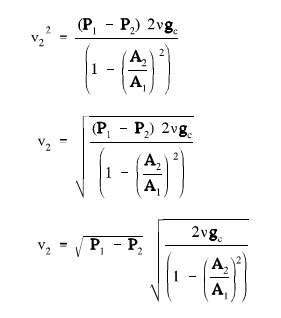
Thus the flow velocity at the throat of the venturi and the volumetric flow rate are directly proportional to the square root of the differential pressure.

The pressures at the upstream area and throat are actual pressures, and velocities from the Bernoulli's equation without a loss term are hypothetical velocities. Whenever losses are considered in the energy equation, the velocities are real velocities. At first, with the Bernoulli equation (i.e., without a head-loss term), the hypothetical velocity at the throat is acquired. Then by multiplying this by the venturi factor (C_v), that accounts for friction losses and equivalents 0.98 for most of the venturis, the real velocity is acquired. The real velocity times the actual region of the throat determines the real discharge volumetric flow rate.

The pressure drop, P₁-P₂, across the venturi can be employed to measure the flow rate by using a U-tube manometer as shown in above figure. The reading, R', of the manometer is proportional to the pressure drop and therefore the velocity of the fluid.