Tension due to Centrifugal Forces:

The belt contains mass and as it rotates along the pulley this is subjected to centrifugal forces. If we suppose that no power is being transmitted and pulleys are rotating, the centrifugal force shall tend to pull the belt as illustrated in Figure (b).

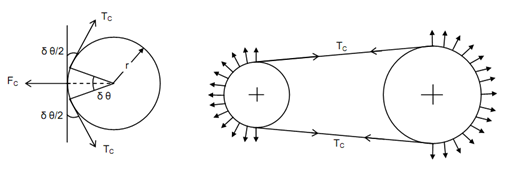
(a)                                                                 (b)

Assume 'T_C' is the tension because of centrifugal forces or it is also known as centrifugal tension. Consider a small element that subtends an angle δθ at the centre of the pulley. Assume 'm' be the mass of the belt per unit length of the belt in 'kg/m'.

The centrifugal force 'F_c' on the element shall be given by following

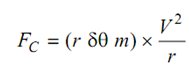
Here V is speed of the belt in m/sec. and r is the radius of pulley in 'm'. Determining the forces on the element normal to the tangent

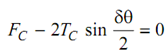
As δθ is very small.

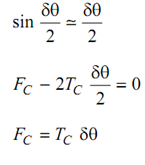
By putting for FC        

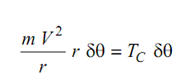
or,

 T_C  = m V ²                        . . . (8.13)

 Thus, by considering the influence of the mass of the belt the tension on the tight side while power is transmitted is given by following

Tension of tight side T_t  = T₁  + T_C and tension on the slack side T_s  = T₂  + T_C .

 The centrifugal tension contain an effect on the power transmitted due to maximum tension may be only T_t that is

T_t  = σ_t  × t × b

∴ T₁ = σ_t  × t × b - m V²