Cone Pulleys:

Sometimes the driving shaft is driven through the motor that rotates at constant speed however the driven shaft is designed to be driven at different speeds. It can be easily completed using stepped or cone pulleys as illustrated in Figure. The cone pulley contains different sets of radii and they are decided such that the similar belt may be utilized at different sets of the cone pulleys.

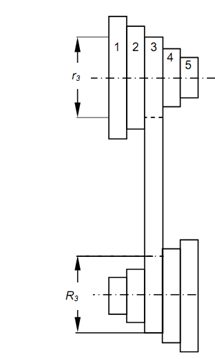
Assume N_d be the speed of the driving shaft that is constant.

N_m be the speed of the driven shaft while the belt is on n^th step.

r_n be the radius of the n^th step of driving pulley.

R_n be the radius of the n^th step of the driven pulley. Where n is an integer i.e., 1, 2, . . .

The speed ratio is inversely proportional to the pulley radii

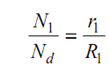       . . . (8.3)

 For this first step radii r₁ and R₁ can be selected conveniently.

 For second pair

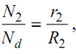, and likewise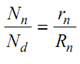

In order to utilize same belt on all of the steps, the length of the belt must be same

i.e.  L₁  = L₂  = .. . = L_n                                 . . . (8.4)

 Therefore, two equations are available - one provided through the speed ratio and other provided through the length relation & for chosen speed ratio, the two radii may be calculate. Also it needs to be kept in mind that the two pulleys are similar. It is wanted that the speed ratios must be in geometric progression.

Assume k be the ratio of progression of speed.

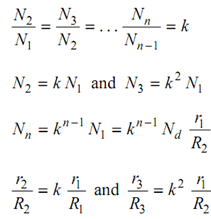
As, both of the pulleys are made alike.

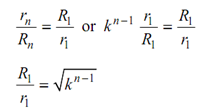                     . . . (8.5)

 If radii R₁ and r₁ have been selected, the above equations provide value of k or vice-versa.