Ratio of Tensions:

Consider a flexible belt wrapped around a portion of a drum. Let the angle of contact be α. Let T₁ and T₂ be the tensions in the belt as shown in Figure, while the motion is just developed between the belt and the drum. If T₁ > T₂, then the impending motion of the belt shall be clockwise relative to the drum. Let a small element of the belt, of length ds subtending an angle dθ at the centre. The free body diagram of this particular element is illustrated in Figure. T and T + δT are the tensions at P and Q, respectively and dN is the normal reaction between the belts as illustrated. The friction force is (μ dN) acting as illustrated.

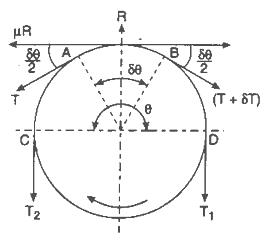
Resolving all of forces tangentially and applying equation of equilibrium, we contain the following

∑ F_t = 0

∴ - T cos (d θ/2) + (T + δT ) cos (d θ/2) - μ dN = 0

∴ δT cos (d θ/2) = μ dN

∴ δT = μ dN

 (∴ d θ is small, cos (d θ/2) → 1)

Likewise, resolving all forces in normal direction, we have following

∑ F_n  = 0

∴ - T sin (d θ/2) - (T + δT ) sin (d θ/2) + dN = 0

∴ - 2T sin (d θ/2) - δT sin (d θ/2) + dN = 0

For small angles, sin θ → θ

∴ - Td θ - δT (d θ/2) + dN = 0

∴ Td θ = d N (neglecting very small quantity δT . (d θ/2) )

From Eq. (17) and Eq. (18), we have following

δT/ T  = μ d θ

Integrating both sides around the portion of belt in contact with the drum, we have following

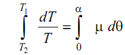
∴ loge( T₁ /T₂) = μ α

∴ T₁ / T₂ = eμα

Therefore, it is seen that the ratio of tensions based only on the angle of wrap α and the coefficient of friction μ.

The torque developed by the belt as a consequence of friction is given as under :

              Torque = T₁ r - T₂ r = (T₁  - T₂ ) r

In fact, if the belt or rope is slipping, the coefficient of static friction must be replaced by coefficient of kinetic friction.

The belts utilized are sometimes V-shaped. The contact among belt and pulley takes place along the sides of the grove. If β is the angle among these two surfaces of contact then the magnitude of the total friction force working on the element will be 2 dF and the sum of the components of the normal forces is 2 dN sin β /2. Proceeding on similar lines, therefore we get,

                                                    T₁/ T₂   = e ^{μα cosec (β/2)}