Definition:

We now want to define an equilibrium concept for static Bayesian games. To do so, we must first define the players' strategy spaces in such a game. Given the timing  of  a  static Bayesian game,  in  which nature begins the game  by drawing the players' types,  a  (pure) strategy for player  i  must  specifL a feasible action for each of player i's possible types.

Definition: In  the static Bayesian game

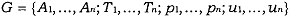, a strategy for player i  is a function s,(t,),  where for each type t,  in T,,  s,(t,)  specifies  the action form the feasible set A,  that type t, would choose if drawn by  nature.

Definition: In a separating strategy each type ti  in Ti  chooses a different action a,  from Ai.

Definition: In a pooling strategy all types choose the same action.

Definition: In  the static Bayesian game

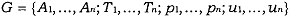,  the strategies

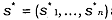
  are (pure strategyj Bayesian Nash equilibrium if for each player i and for each of i's  types t, in T_i, s*_i(t_i)  solves

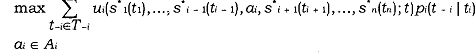
That  is, no  player wants  to  change  her  strategy, even  if  thi change involves only one action by  one type.

It can  be  shown that  in  a  finite static Bayesian game there exists a Bayesian Nash equilibrium, perhaps in mixed strategies.