Multiple Basing-point System:
The excess profits ('phantom freight' gains) realised by the firms selling at the basing-point price to buyers located at places where this price is higher than their production costs plus transportation cost, may be reduced under a system of multiple basing pricing. In such a system, several places are agreed as basing points. The delivered price of all oligopolists will be the same for buyers located in a certain place and will be the lowest possible delivered price. This is illustrated in the Figure.
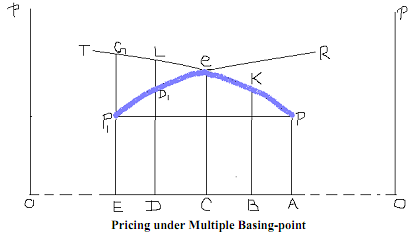
To illustrate the multiple Basing-point system assume that the locations A and E are both agreed as basing-points. The delivered price of firms in location A are those on the curve PT (same as in Figure). The delivered prices of firms in location E are those on the curve P1R. Only at the point of intersection of PT and P1R (i.e., point e) will the delivered prices be identical for firms located in E and A. To the left of e the delivered price of firm in A are higher than those of firms located in E; thus for buyers located to the left of e the delivered prices quoted by all sellers will be the (lower) prices of curve P1e. To the right of point e the delivered prices of firms in A are lower, and these will be quoted by all firms to the buyers. In this way, the relevant delivered prices for buyers located between E and A are on the segments P1e (of P1R) and eP (on PT). A firm located in A will charge the delivered price on P1e to buyers located between E and C, without gaining any 'phantom freight'. If this firm wants to sell to buyers located further than C, it will have to cover itself part of the freight. This would not at all be profitable because beyond e, prices are low for firm A and the price charged will not cover the freight charge.
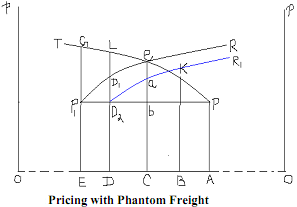
Only the firms between the basing points will have 'phantom frieghts', given that they can produce at the same mill price as firms in A or E. For example, a firm located in D will charge the delivered price Coe to buyers located at C, and will receive 'phantom freight' equal to ae, as per the freight curve is represented by the curve D2R. A firm located at C and selling to local customers will receive a greater phantom price (equal to eb) given the two basing-point pricing arrangement. This is illustrated in Figure.
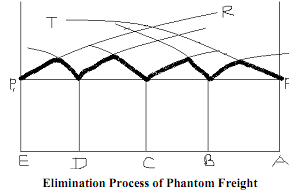
As the number of basing-point increases, the phantom freights are gradually eliminated. In the limit, if sellers were located next to each other and there were as many basing points as sellers, all would quote the same price EP1 = AP, which is the lowest of delivered prices of all sellers. This is shown in Figure. In the figure, let us suppose that B, C and D are all basing-points. Therefore, as before the price to be charged by the oligopolists would be the lower of the prices charged by each. This is shown by the bold line. Now as the number of basing-points increases the price line will fall further and finally coincide with the mill price AP = EP1.