Scaling:

Scaling changes the size of the object. Let S_x & S_y as the scaling factors in x and y direction and S_F be the entire scaling factor. Then after the scaling (taking into account the scaling factors) the coordinates of the point (x, y) alters to (x′, y′).

x′ = x* S_x

y′ = y* S_y

If SF > 1.0, then the object get larger. If S_F < 1.0, then the object get smaller. If S_x = S_y, then we contain uniform scaling and this maintains the relative proportions of the object. If S_x ≠ S_y, then we contain differential scaling and this deforms the object.

Different Scaling around x and y-Axes

S_x = 0.5; and S_y = 1.5

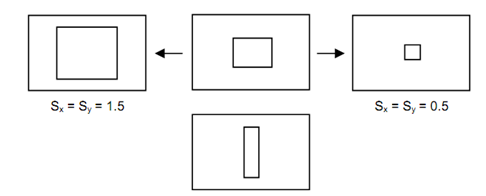
Figure: 2-Dimensional Scaling