Homogeneous Coordinates:

Transformation of each point in the two-dimensional plane may be accomplished by translating the origin or any other point in the two dimensional plane, that is

               X* = ax + by + m

                Y* = bx + dy + n

But this is not possible to introduce the constants of translation m, n into the general 2 × 2 transformation matrix. To conquer this, homogeneous coordinates are introduced.

A point (x, y) may be converted to homogeneous coordinates by multiplying with 1/w that means the homogeneous form becomes [x/ w, y/ w, 1 / w]. Let the value of w approaches to zero, then [x/ w, y/ w] moves farther and farther away in the direction of (x, y). While w becomes zero [x/ w, y/ w] moves to infinity. Thus, we would say, the homogeneous coordinates (x, y, 0) is the ideal point or point of infinity in the direction of (x, y). It must also be noted down that a point (x, y, w) in homogeneous plane while converted to the corresponding point in (x, y) plane it would be [x/ w, y / w]. For instance, (6, 8, 10) in homogeneous plane would convert to (6/10, 8/10) = (0.6, 0.8) in xy plane if w = 10. But the homogenous coordinates of a point (x, y) is (xw, yw, w) for any non-zero w. Thus, a point (3, 2) may be converted to [6, 4, 2] or [12, 8, 4] etc.

Thus, converting from homogeneous coordinates to conventional is unique but changing a conventional to homogeneous one is not unique.

Thus the general transformation matrix would be

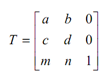
By utilizing the concept of homogeneous coordinates system this is possible to rotate or even reflect respectively through any arbitrary point or line.

Generally, rotation through any arbitrary point may be achieved by first translating the point to its origin, performing the needed rotation and then translating back to the original centre of rotation.