2-Dimensional Shear:

In scaling and reflection only the diagonal terms are affected. Although in case of shear transformations a shape distortion takes place.

The X-direction shear is specified by the following matrix :

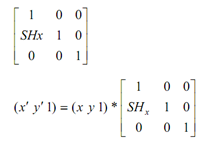
where SH_x generates a shearing along x that is proportional to y :

x ′ = x + SHx   * y and y′ = y,  that means 1 = 1

Now let us assume a transformation matrix 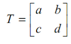and a point A = [x, y].

If a = d = 1 and c = 0,

then,

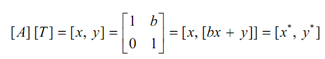
It is apparent that y* depends linearly on the original co-ordinate.

And Y-direction shear is specified by the following matrix :

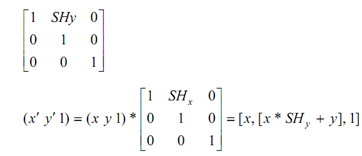
where SH_y generates a shearing along y that is proportional to x :

x′ = x

y′ = x * SH_y   + y

1 = 1

After explaining all the transformations above, it is significant to understand the effect of these transformations on the origin, that is

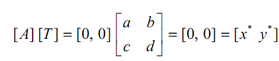
∴  This is apparent from the above equation that the origin is invariant.

A number of transformations that means rotation, translation scaling represented by [2 × 2] transformation matrix have already been discussed above. It should be clear to you from the above discussion that the origin of the coordinate system is invariant with respect to all of these transformations. But sometimes it becomes essential to modify the position of origin. This may be accomplished by introducing the concept of homogeneous coordinates.