2-Dimensional Rotation:

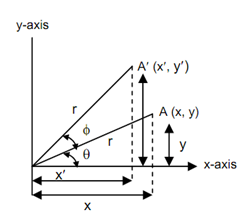
Let us assume a case of a 2-D rotation through an angle φ where the coordinates x, y are translated to x′, y′. Note down that φ is positive for a counter clockwise rotation and that rotation is around the origin (0, 0).

Figure

Now, derive the formula for 2-D rotation.

Consider a point A whose coordinates are (x, y) & after the rotation of A through an angle φ coordinates of A′ are (x′, y′)

θ = Initial angle, φ = Angle of rotation.

∴ Initial cartesian co-ordinates are

x = r cos θ

y = r sin θ

x′= r cos (θ + φ) = r cos θ cos φ - r sin θ sin φ.

y′ = r sin (θ + φ) = r sin θ cos φ + r cos θ sin φ.

Hence, x′ = x cos φ - y sin φ

y′ = y cos φ + x sin φ

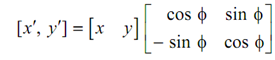
If rotation is to be carried out around any point other than the origin, for example. the centre of an object, then solution to this problem is to carry out various transformations instead of just one.

Therefore, the transformation matrix for a general rotation about the origin by an arbitrary angle φ is following

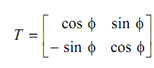
Rotations are assumed positive in the direction of counter clockwise around the origin.