Working with truth tables

Truth tables are, infinitely versatile in theory. It is possible to construct or break down the logic operations of any complexity by using these tables, given that you have lots of paper and a fondness for column-and-row matrix drawing. Computers can be programmed to work with the truth tables, although displays and printouts get horrible to deal with if the logic functions are quite messy.

Building up
You can build up complex logic operations up simply by means of a truth table. An example of such type of building process is shown in the Table given below.There are 3 variables X, Y, and Z. Each can be either0 or 1 /low or high. All the possible combinations are listed by writing the binary numbers XYZ upwards  from 000 through 111. This forms the 1st column of the truth table. If there are n total variables, thus there will be 2n possible combinations.

The second column lists values of X+Y, the OR function. Some rows are duplicates of each other; you write all resultants down anyway.The third column lists negations of values in the 2nd column; this is the NOR operation − (X+Y). The fourth column shows values of XZ.The fifth column is disjunction of the values in the 3rd and 4th column. It renders values for complex logic operation − (X+Y)+ XZ.

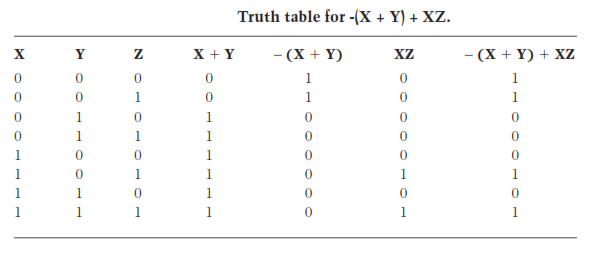
Breaking down
Assume that you were called upon to break down a logical operation, rather than to build it up. This is kind of problem encountered by engineers. In the process of designing digital circuit, the engineer is faced with figuring out what combination of logic gates will yield complex operation, say, XY +− (XZ)+YZ.
Proceed by listing all possible logic states for the 3 variables X, Y, and Z, exactly as in the Table given below. Then find values of XY (X AND Y), listing them in the 4th column. Next, find values XZ and list them in a 5th column. Negate these values to form a 6th column, depicting − (XZ). Next, find the values YZ and list them in a 7th column. Finally, perform OR operation on values in the columns for XY, − (XZ), and YZ. A multiple-valued OR is 0 only if all the individual variables are 0; if any or all of inputs are 1, then output is 1.

This process yields the table given below.

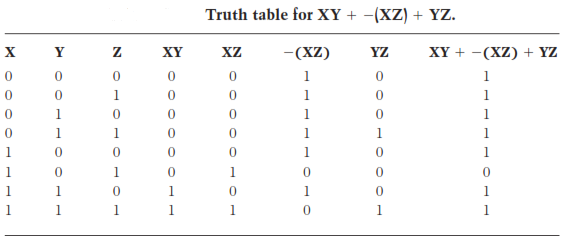
This is a bit like middle-school algebra, isn’t it? The rules of algebra can, with certain adjustments, be directly applied to the digital logic operations. This is called as Boolean algebra, named after mathematician Boole who 1st devised it as an alternative to truth tables