Numbering systems

Any number, like 35912, can be rendered in some other number base or modulus. Then it is written differently. But it is always the same quantity.

The decimal system
In decimal number system, each digit 0 through 9 represents itself, or else itself times some power of 10. The value of digit depends on the position or place in number. In the case of the number 35912, the digit 2 is in the units place, and has value of 2. The digit 1 is in the 10s place; it takes value of 1X 10¹=10. The digit 9 is in the 100s place, having the value of 9 × 10²⁼900. The digit 5 is in 1,000s place, and represents 5X10³ =5000. The digit 3 is in 10,000s place, and has a value of 3X10⁴   30,000. The total value is sum of all these: 2+10+900  
5,000+ 30,000=35,912.

A decimal number is represented in digital form, but it requires 10 possible states. Any of the decimal number having a binary equivalent which is composed of digits which are all 0 or 1: just 2 different possible states.

Modulo what?
You most likely learned modular arithmetic in elementary school. If so, you should remember working with modulo 8 , or modulo 1), or base 4, or 12, or 20. In the computer electronics, octal and hexadecimal numbers are encountered occasionally, in addition to the decimal numbers.

At some times, special interest groups have tried to get whole world to switch to some modulus besides 10. Some people think that base 12 must be used. Others believe that base 20 makes most sense. Still others argued for the base 8 or base 16 as these values are elegant: they are repeatedly cut in half all the way down to 1.

The Binary system
Binary numbers are in modulo 2. In this system, digits are all either 1 or 0, and the places go in powers of 2. Hence, to the immediate left of the units place is 2’s place (21), then the 4’s Place(22), then the 8’s place (23), and so on. In Table given below, powers of 2 are represented up to 215.

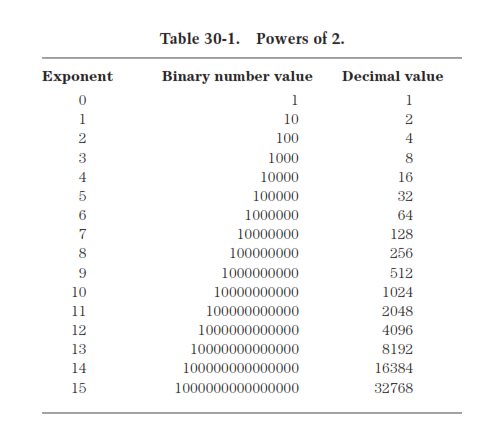
Generally the nth place from right has the decimal value 2n. The total decimal value, for the given binary number, is sum of the decimal values of each of the places.

Converting decimal numbers to binary form is done by using the Table given below. Assume, for instance, that you want to convert 35912 to binary notation. Firstly, find the largest decimal number on table which is no greater than the decimal number you wish to convert. In this case, it is 32768    215. From this, you know that there are16 digits in the binary representation of this number, one for every place 20 through 215. Mark off 16 slots on a sheet of paper, and place the digit “1” in left space, representing 215.

Now, use the Table given below to determine which number is added to 32768 to get the greatest decimal number which does not exceed 35912. It happens to be 2048    211. Place digits “0” in slots for 214, 213, and 212. Then place “1” in space for 211.If  you  continue  this  process,  you will ultimately get  the  binary  number 1000110001001000. The 16-digit binary number is equal to decimal 35912    8 64    1024    2048    32768    23    26    210 + 211    215. The slots for the exponents 3, 6,10, 11, and 15 each are filled with the binary digit 1; the others are filled with the binary digit 0.

It is likely to have fractional values in the binary notation, as it is in decimal notation. The first place to the right of the point is the 1/2’s place (2-1). The next place is the 1/4’s place (2-2); then comes the 1/8’s place (2-3), and so on. Thus, 0.001 in binary notation represents the decimal fraction 1/8. You can think of it as dividing the size in half as you progress towards right repeatedly.

Why use such cumbersome notation?
Perhaps you have noticed that binary notation gets into long number strings. This is true. But computers do not have trouble dealing with long strings of digits. To a computer, the significant thing is to be certain of value of each digit. This is easiest when the attainable states are as few: two. High or low, Logic 1 or 0, On/off.