Twist vector:

The twist vector may be written in terms of its Cartesian components as following

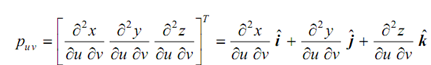
                                                                                     u_min   ≤ u ≤ u_max , v_min   ≤ v ≤ v_max

The twist vector based on both surface geometric characteristics and its parameterization. Because of the concluding dependency, interpreting the twist vector in geometrical terms can be misleading since p_uv ≠ 0 does not essentially imply a twist in a surface. For instance, a flat plane is not a twisted surface. Though, Based on its parametric equation, p_uv can or cannot be zero.

The normal to a surface is another significant analytical property. It is utilized to calculate cutter offsets for three-dimensional NC programming to machine surfaces, volume calculations, & shading of surface model. The surface normal at any point is - a vector that is perpendicular to both tangent vectors at the point that means,

N (u, v) =         (∂p /∂u )× (∂p/ ∂v) = p_u × p_v

and the unit normal vector is specified by

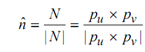
In the above equation the order of the cross-product may be reversed and still defines the normal vector. The sense of N, or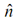, is selected to suit the application. In machining, the sense of 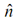is usually selected so that 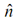points away from the surface being machined. In volume calculations, the sense of 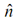is selected positive while pointing toward existing material and negative while pointing to holes in the part.

 The surface normal is zero when p_u × p_v = 0. This takes place at points lying on a cusp, ridge, or a self-intersecting surface. It may also occur while the two derivatives p_u and p_v are parallel, or while one of them has a zero magnitude. The latter cases correspond to a pathological parameterization, which may be remedied.