Tangent vector:

The tangent vector concept may be extended to surfaces. The tangent vector at any particular point P (u, v) on the surface is attained by holding one parameter constant and differentiating w.r.t. the other. Thus, there are two tangent vectors, a tangent to each of the intersecting curves passing through the point as illustrated in Figure. These vectors are given by :

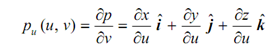           u _min ≤ u ≤ u _max        ,  v _min ≤ v ≤ v _max

along with  the v = constant curve, and

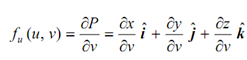                u _min  ≤ u ≤ u _max        ,  v _min ≤ v ≤ v _max

along with  the u = constant curve. These two equations may be combined to give

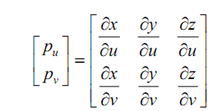
If dot product of the two tangent vectors is equal to zero at any point on a surface, then the two vectors are perpendicular to one another at that point. Figure illustrated the tangent vectors at the corner points of a rectangular patch and at point P_ij. The notation ∂P/∂u |P_ij, for instance, means that the derivative is calculated at the point Pij defined by u = u_i and v = v_j. Tangent vectors are useful in finding boundary conditions for patching surfaces together in addition to defining the motion of cutters along the surfaces throughout machining processes. The magnitudes & unit vectors of the tangent vectors are specified by following

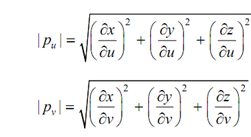
and

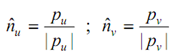
The slopes to a given curve on a surface may be evaluated, although they are less important and seldom utilized in surface analysis.