Rigid and Deformable Solids:

Look at the general swing display in Figure that you would have enjoyed playing along with during your earlier days. While a child sits on the swing we might not perceive any appreciable deformations. But if the iron bars be replaced through bamboo sticks and the iron chain be replaced through rubber strings, we could observe considerable deformations. We might then conclusively say that while forces are applied on solids, deformations are known in them. All solids are deformable solids; therefore, the subject that once was known as Mechanics of Deformable Solids is now easily called Mechanics of Solids.

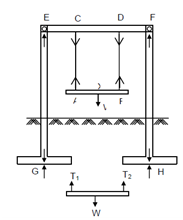
Figure

You might wonder as to why we should have the term rigid solid at all, if within reality, there are no such solids. It has been already described that the word rigid solid is just a conceptual idealisation. There are some significant uses for such idealization. Now consider the analysis of forces in the members of a few of the plane trusses. You were providing the geometry of a structure (that in its totality might be considered as a solid of complex geometry) on that some forces have been presented to act. Although analyzing these structures (solids) for searching out the member forces, the forces in the members have been resolved within their horizontal and vertical elements, supposing that the member orientations have not changed because of the application of external forces. In fact, the orientations of most of the members change, since the structure deforms under the loads.

Therefore, these deformations and thus, the resulting changes in member orientations are so little in which the error in computed member forces are negligibly small. You might think that even these errors might be eliminated through taking into account the deformations too. Other than an attempt to do so will reveal the complexity of the calculations included. The corrections therefore effected are known secondary effects and might be neglected in most of the cases. In the analysis of other kinds of structures also while the whole equilibrium is considered the whole structure or any part under consideration might be treated as a rigid solid.

In several cases, known as determinate problems, the analysis of forces inside a solid could be computed treating it as rigid.