Internal Pressures:

The force P (or R) display in the figures is just the resultant of forces applied over a few areas (small or even full). On any area the force might not be distributed uniformly.

Therefore, we might consider an infinitesimally little area ΔA over that a small part of the total force ΔP might be considered to be uniformly acting.

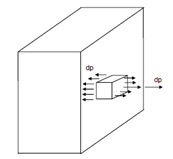
Here, the ratio dP (or rather   ΔP/ ΔA) might be known as pressure (suctional or compressive) at the point. Considering a little element having the area dA on one of its faces as display in Figure, we realize in which this pressure is accompanied through the equilibrium pressure on the opposite face of the element.

Figure

Such a set of internal pressures acting on solids is described as stress. Depending on that set of planes such pressures are applied, there could be a number of such sets and they might be known as stress components (More about this we shall learn later).

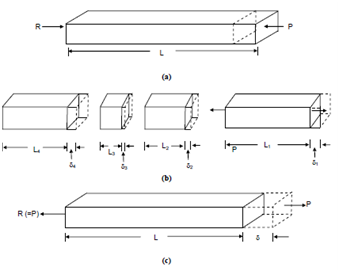
To take the easiest case, if the total force P is uniformly distributed over the cross section A as display in Figure (a), then the magnitude of stress in the solid is P/A. This entity, stress is implies by the symbol 'σ' and commonly expressed in N/mm^² units, also implies as Mega Pascal (MPa) as both are numerically equal.

Now let us turn our attention to deformations. The set of forces P and R (Figure(a)) are pulling the solid within opposite directions. Accordingly the solid gets elongated and let this elongation be implies through the symbol 'δ'. If the forces be applied on the individual components, each element will elongate (Figure(b)) and it has been experimentally built that

(a)        The magnitude of the individual elongations are proportional to the length of every of the elements, and

(b)       The whole elongation of all the elements add up exactly to δ.

Figure

We might conclude in which the ratio of elongation to length of the elements δ1/L1, δ2/L2, is invariable and equivalent to δ/L. This ratio is describing as strain (more specifically as longitudinal strain) and implies through ε. If the forces applied are in the opposite direction, as display in Figure (a), the solid will get its length shortened and the deformation and strain in like a case are considered negative.